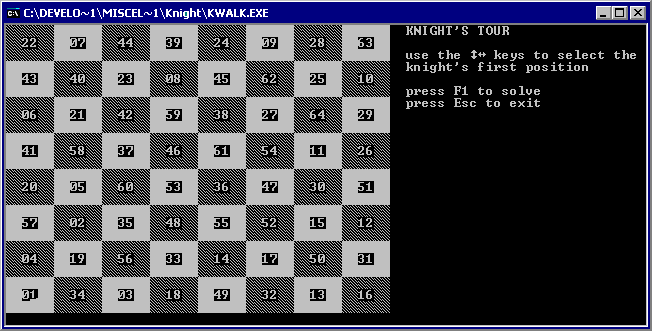
The
knight's tour is when the knight, alone on the chessboard, makes 64 moves,
landing on each square once and only once. A "closed" tour is one
where the knight returns to the starting square. There are several approaches to solving
this problem, including Warnsdorff's rule (always moving to the square having
the fewest onward moves). You push attempts onto the stack, try, and upon failure, return to the next candidate path. This simple algorithm is quite fast and finds
different solutions depending on which square you start.
I have written millions of lines of code but have never sat through a class on computer programming. I had to pass the course to graduate so I made a proposition. The instructor would assign me a problem. If I could solve it, I would get an A and he would never see me again. The year was 1974 and the problem was the knight's tour. Two days later I turned in the solution in FORTRAN on punch cards. I did not know he had been given the problem in graduate school but had never solved it. If I had, I might not have taken the risk. Years later I translated the algorithm into assembler, first for the HP-1000 minicomputer and then for Intel x86. The entire executable code is only 1665 bytes. It is 16-bit and will run on any 32-bit version of Windows (in a command prompt), but will only run on a 64-bit O/S inside a virtual box (not just a command prompt).
The code is available here> knights_tour_16bit.zip The algorithm is also available in C. The core of which is listed below:
int Tour(int x1,int y1)
{
int i,m=0,n1,n2,x2,x3,y2,y3;
while(1)
{
n1=9;
for(i=0;i<8;i++)
{
x2=x1+move[i].x;
y2=y1+move[i].y;
if(!MoveOK(x2,y2))
continue;
if(m==62)
{
x3=x2;
y3=y2;
break;
}
n2=Moves(x2,y2);
board[y2][x2]=0;
if(n2<1||n2>=n1)
continue;
x3=x2;
y3=y2;
n1=n2;
}
if(n1==9&&m!=62)
return(0);
m++;
x1=x3;
y1=y3;
board[y3][x3]=m+1;
if(m==63)
break;
}
return(1);
}
The complete code is available here> knights_tour_inC.zip
I also have a 3D version using OpenGL shown here:

The code is available here> knights_tour_in_3D.zip The animated result is shown below:

The same algorithm in FORTRAN is provided here> Knights_tour_FORTRAN.zip